4. Areas

When finding areas, you measure from the centre outwards rather than from x-y axis

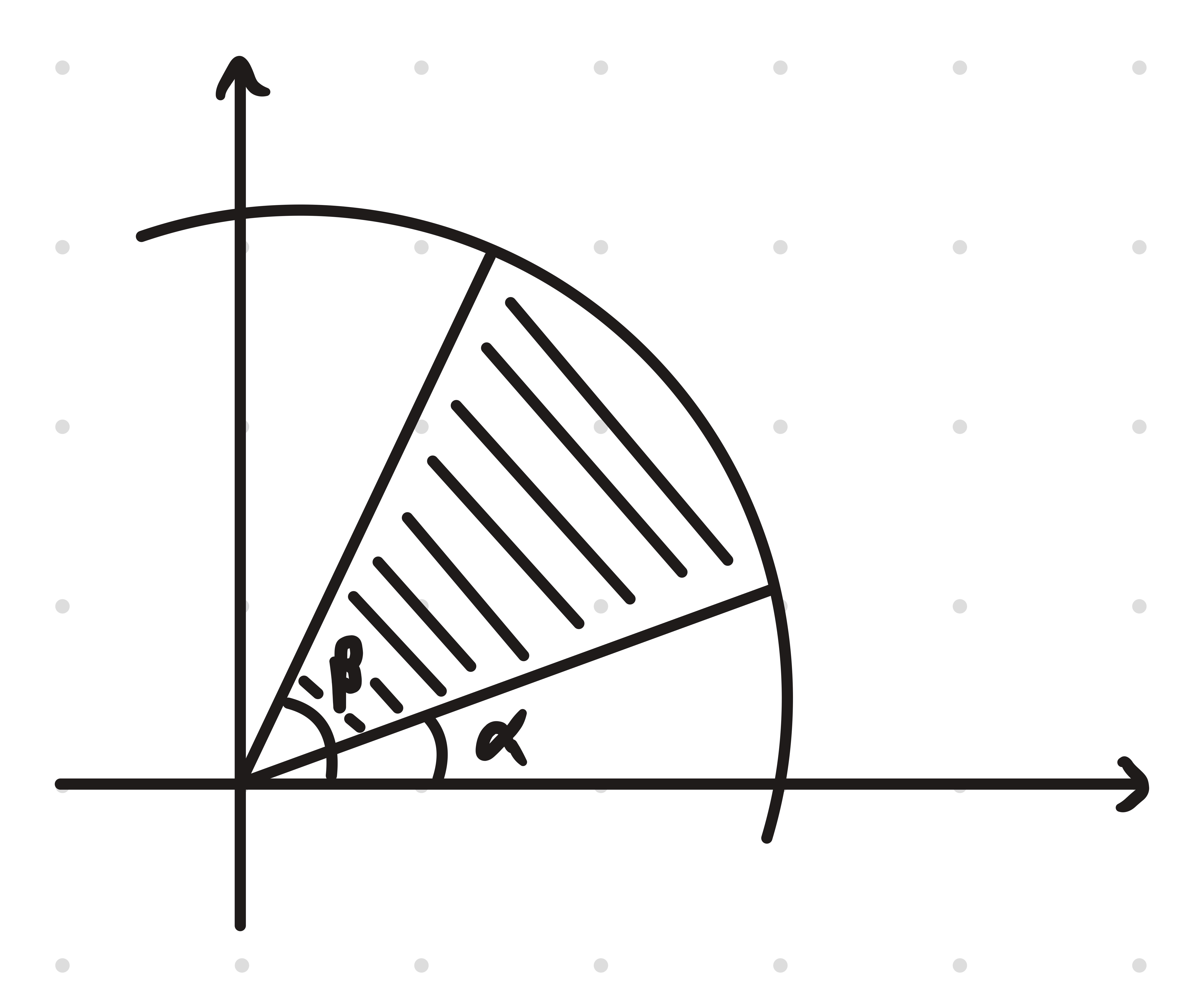
area of a sector

$$\text{area} = \dfrac{1}{2}r^2 \theta$$

integrating from $\alpha$ to $\beta$

$$\text{area} = \dfrac{1}{2} \int_{\alpha}^{\beta} r^2 \; d\theta$$

Example

Find the area enclosed by $r = a(1 + \cos \theta)$

Answer

$$\text{area} = \dfrac{1}{2} \int_{0}^{2\pi} a^2(1 + 2\cos \theta + \cos^2 \theta) \; d\theta$$

pull out the $a^2$ and integrate

$$\text{area} = \dfrac{a^2}{2} [\dfrac{3\theta}{2} + 2\sin \theta + \dfrac{1}{4}\sin 2\theta]_{0}^{2\pi}$$

simplifies to

$$\text{area} = \dfrac{3\pi a^2}{2}$$

another way to do this is to integrate from $0$ to $\pi$ and multiply by $2$

this is possible because we know this equation is symmetrical

$$\text{area} = \int_{0}^{\pi} a^2(1 + 2\cos \theta + \cos^2 \theta) \; d\theta$$