2. Polar to Cartesian
-----
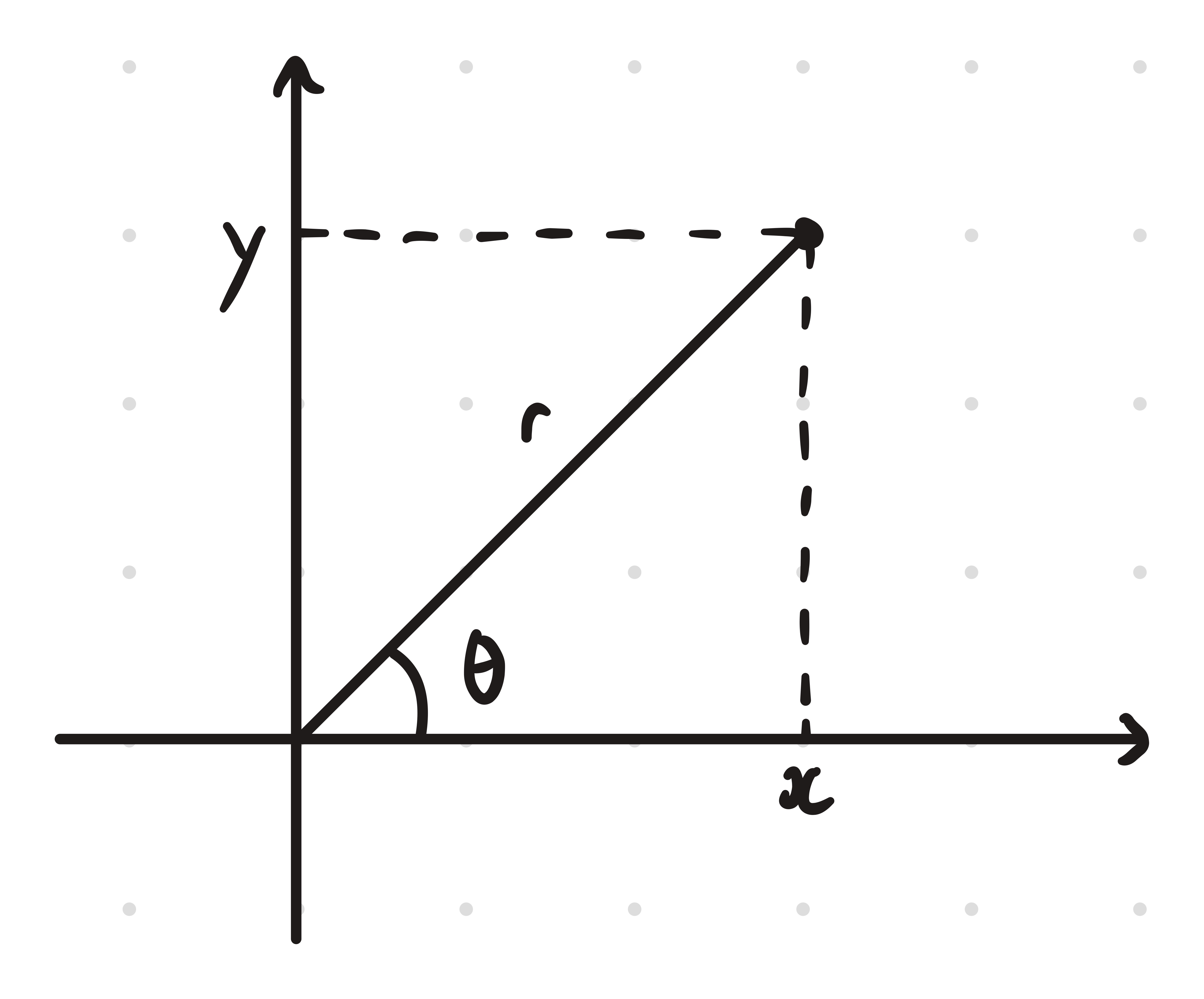
Conversions
Example 1
Convert the polar coordinate in their cartesian form
Answer
Example 2
Convert the cartesian coordinate into its polar form
Answer
-----

Convert the polar coordinate in their cartesian form
Convert the cartesian coordinate into its polar form